Carolyn drew a rhombus abcd. fill in the blanks. – As we delve into the topic of “Carolyn Drew a Rhombus ABCD: Fill in the Blanks,” we embark on a journey of geometrical exploration. Rhombuses, with their unique properties and applications, present an intriguing subject for academic inquiry.
This discourse will delve into the fundamental characteristics of rhombuses, examining their equal sides and opposite angles. We will explore the construction of rhombuses using a ruler and compass, unraveling the formulas for calculating their area and perimeter.
Rhombus Properties
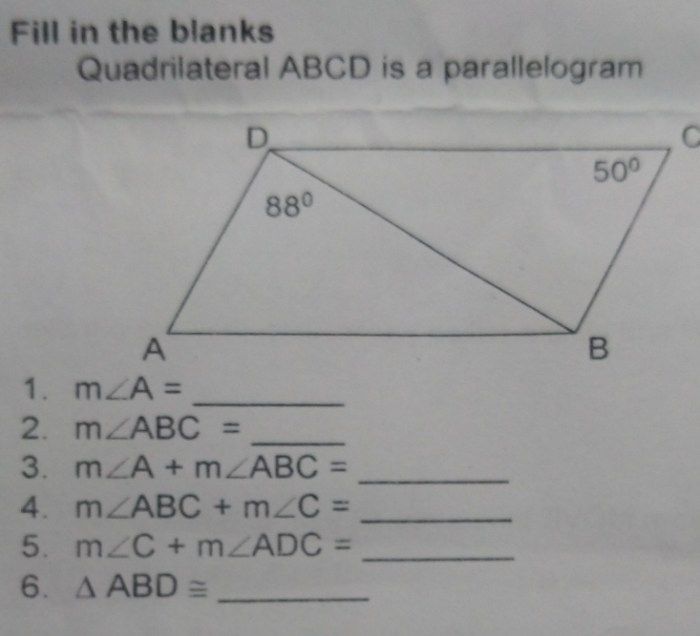
A rhombus is a two-dimensional shape with four equal sides and opposite angles that are equal. Rhombuses are a type of parallelogram, which means they have two pairs of parallel sides.
The properties of a rhombus include:
- All four sides are equal in length.
- Opposite angles are equal in measure.
- Diagonals bisect each other perpendicularly.
- Diagonals divide the rhombus into four congruent right triangles.
Rhombus Construction
To construct a rhombus using a ruler and compass, follow these steps:
- Draw a line segment of any length.
- Using the compass, set the radius to half the length of the line segment.
- Place the compass point at one end of the line segment and draw an arc above and below the line segment.
- Repeat steps 3 and 4 at the other end of the line segment.
- Connect the endpoints of the arcs to form the rhombus.
The length of the sides of the rhombus is equal to the length of the original line segment. The length of the diagonals can be calculated using the Pythagorean theorem.
Rhombus Area and Perimeter
The area of a rhombus can be calculated using the formula:
Area = (1/2)
- d1
- d2
where d1 and d2 are the lengths of the diagonals of the rhombus.
The perimeter of a rhombus can be calculated using the formula:
Perimeter = 4s
where s is the length of one side of the rhombus.
Rhombus in Coordinate Geometry
A rhombus can be represented on a coordinate plane by plotting the coordinates of its vertices. The vertices of a rhombus are typically given as (x1, y1), (x2, y2), (x3, y3), and (x4, y4).
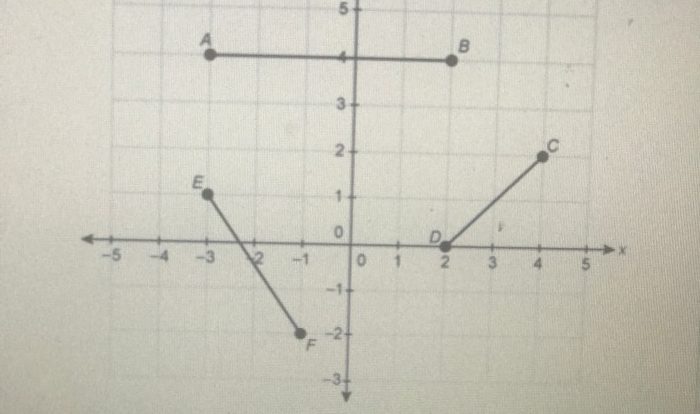
The coordinates of the vertices of a rhombus can be used to find the length of its sides and diagonals. The distance between two points (x1, y1) and (x2, y2) is given by the formula:
Distance = sqrt((x2
- x1)^2 + (y2
- y1)^2)
Rhombus Applications
Rhombuses are found in a variety of everyday objects, including:
- Diamonds
- Baseball diamonds
- Chessboards
- Kites
- Roofs
The properties of rhombuses make them suitable for a variety of applications. For example, the equal sides of a rhombus make it a good shape for a baseball diamond, and the perpendicular diagonals of a rhombus make it a good shape for a kite.
FAQ Explained: Carolyn Drew A Rhombus Abcd. Fill In The Blanks.
What is the definition of a rhombus?
A rhombus is a quadrilateral with four equal sides.
How do you construct a rhombus using a ruler and compass?
Draw two intersecting lines to form the diagonals of the rhombus. Then, using a compass, draw circles with the same radius centered at each intersection point. The points where the circles intersect will be the vertices of the rhombus.
What is the formula for calculating the area of a rhombus?
Area = (1/2) – d1 – d2, where d1 and d2 are the lengths of the diagonals.