Embark on an educational journey with our engaging surface area of pyramids and cones quiz! This comprehensive assessment delves into the intricacies of calculating the surface areas of these geometric solids, equipping you with a deeper understanding of their mathematical properties.

Throughout this quiz, you’ll explore the formulas, examples, and applications of surface area calculations, gaining valuable insights into their significance in various fields.

Surface Area of Pyramids

The surface area of a pyramid is the sum of the areas of its base and its lateral faces. The base of a pyramid can be any polygon, but the lateral faces are always triangles.

The formula for calculating the surface area of a pyramid is:

$$A = B + \frac12Pl$$

where:

• A is the surface area of the pyramid
• B is the area of the base of the pyramid
• P is the perimeter of the base of the pyramid
• l is the slant height of the pyramid

The slant height is the distance from the vertex of the pyramid to the midpoint of one of its edges.

Examples of different types of pyramids and their surface areas

• Square pyramid: A square pyramid has a square base and four triangular lateral faces. The surface area of a square pyramid is:

$$A = B + 4\frac12Pl$$

• Triangular pyramid: A triangular pyramid has a triangular base and three triangular lateral faces. The surface area of a triangular pyramid is:

$$A = B + 3\frac12Pl$$

• Pentagonal pyramid: A pentagonal pyramid has a pentagonal base and five triangular lateral faces. The surface area of a pentagonal pyramid is:

$$A = B + 5\frac12Pl$$

Relationship between the base area and the surface area of a pyramid

The base area of a pyramid is directly proportional to the surface area of the pyramid. This means that as the base area of a pyramid increases, the surface area of the pyramid also increases.

Surface Area of Cones

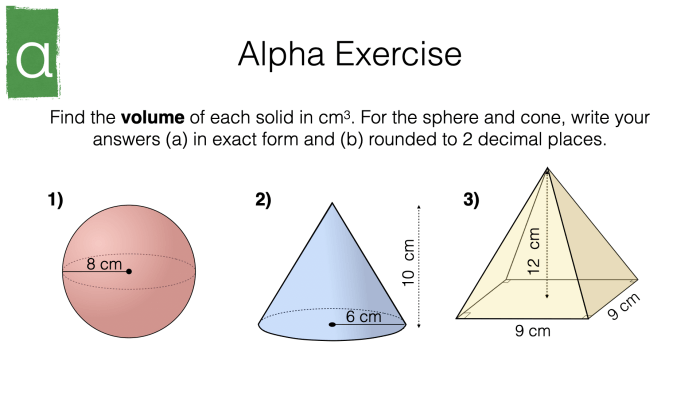
The surface area of a cone is the sum of the areas of its base and its lateral surface. The base of a cone can be any circle, but the lateral surface is always a cone-shaped surface.

The formula for calculating the surface area of a cone is:

$$A = B + \pi rl$$

where:

• A is the surface area of the cone
• B is the area of the base of the cone
• r is the radius of the base of the cone
• l is the slant height of the cone

The slant height is the distance from the vertex of the cone to the edge of the base.

Examples of different types of cones and their surface areas, Surface area of pyramids and cones quiz

• Right circular cone: A right circular cone has a circular base and a vertex that is directly above the center of the base. The surface area of a right circular cone is:

$$A = \pi r^2 + \pi rl$$

• Oblique circular cone: An oblique circular cone has a circular base and a vertex that is not directly above the center of the base. The surface area of an oblique circular cone is:

$$A = \pi r^2 + \pi rl\sqrt1 + \left(\frachr\right)^2$$

• Truncated cone: A truncated cone is a cone that has had its top cut off. The surface area of a truncated cone is:

$$A = \pi r_1^2 + \pi r_2^2 + \pi l\sqrtr_1^2 + r_2^2 + l^2$$

Relationship between the base radius and the surface area of a cone

The base radius of a cone is directly proportional to the surface area of the cone. This means that as the base radius of a cone increases, the surface area of the cone also increases.

Comparing Surface Areas of Pyramids and Cones

The surface areas of pyramids and cones are similar in that they are both calculated by adding the area of the base to the area of the lateral faces. However, the formulas for calculating the surface areas of pyramids and cones are different because the shapes of the lateral faces are different.

Pyramids have triangular lateral faces, while cones have cone-shaped lateral surfaces. This difference in shape results in different formulas for calculating the surface areas of pyramids and cones.

Examples of real-world objects that are shaped like pyramids and cones

• Pyramids: The Great Pyramid of Giza, the Louvre Pyramid
• Cones: Ice cream cones, traffic cones, party hats

Applications of Surface Area Calculations

Surface area calculations are used in a variety of fields, including architecture, engineering, and manufacturing.

• Architecture:Architects use surface area calculations to determine the amount of materials needed to build a structure. For example, an architect might need to calculate the surface area of a roof in order to determine how many shingles are needed.

• Engineering:Engineers use surface area calculations to design and build machines and structures. For example, an engineer might need to calculate the surface area of a heat exchanger in order to determine how much heat it can transfer.
• Manufacturing:Manufacturers use surface area calculations to determine the amount of material needed to produce a product. For example, a manufacturer might need to calculate the surface area of a metal sheet in order to determine how many pieces can be cut from it.

Surface area calculations are an important tool in a variety of fields. By understanding how to calculate surface area, you can solve real-world problems and design and build better products.

User Queries: Surface Area Of Pyramids And Cones Quiz

What is the formula for calculating the surface area of a pyramid?

Surface Area = Base Area + (1/2) – Perimeter of Base – Slant Height

How do you find the surface area of a cone?

Surface Area = πr² + πrl

What are some real-world applications of surface area calculations?

Architecture, engineering, manufacturing, packaging