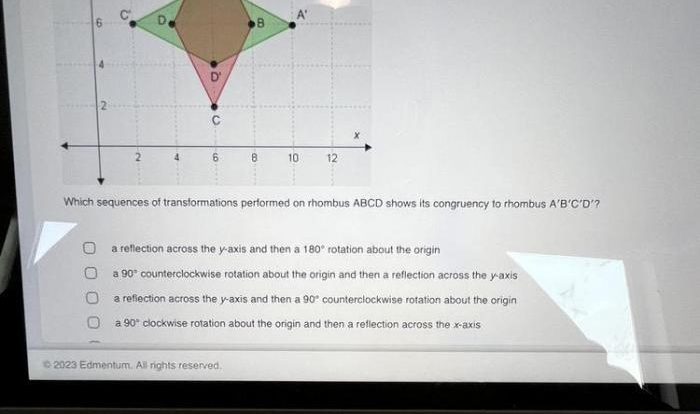
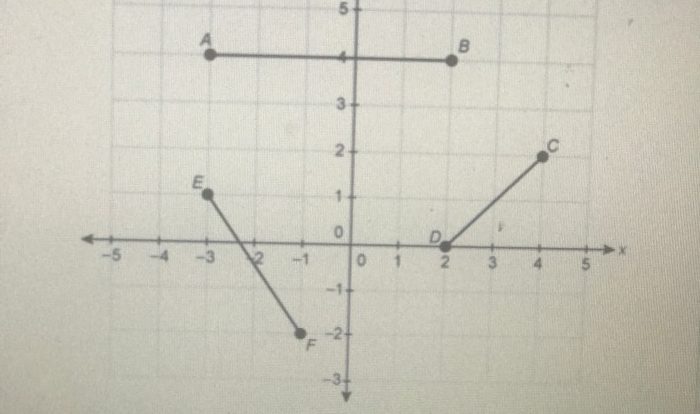
Embark on an enlightening journey into the realm of unit 4 test congruent triangles answers, where we unravel the intricacies of triangle congruence, its properties, and its diverse applications. This comprehensive guide delves into the fundamental concepts of congruent triangles, empowering you with a thorough understanding of their significance in the world of geometry.

Through meticulous explanations and illustrative examples, we explore the three triangle congruence theorems—SSS, SAS, and AAS—and delve into the methods for proving triangle congruence, such as angle bisectors, perpendicular bisectors, and medians. Discover how these theorems and methods are applied in real-world scenarios, particularly in construction, engineering, and design.

1. Congruent Triangles

Definition and Properties

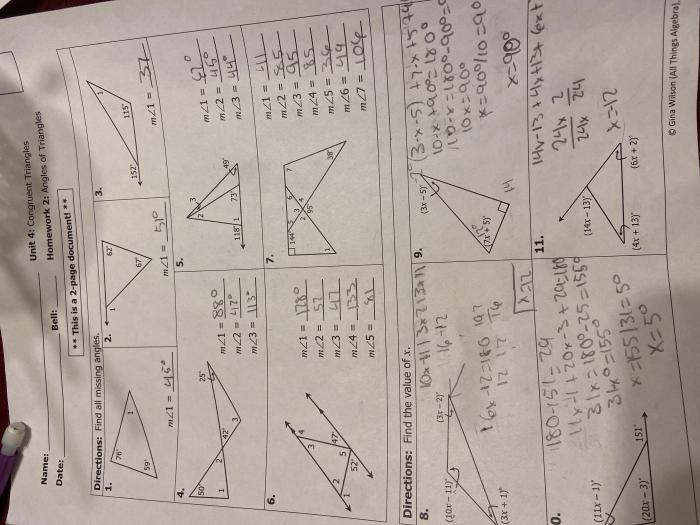
Congruent triangles are two triangles that have the same shape and size. They have equal corresponding sides and angles.

• Definition:Two triangles are congruent if and only if their corresponding sides and angles are equal.
• Properties:Congruent triangles have the following properties:
• Equal corresponding sides
• Equal corresponding angles
• Equal areas
• Equal perimeters

Examples:The following pairs of triangles are congruent:

• Triangles with three equal sides (equilateral triangles)
• Triangles with two equal sides and two equal angles (isosceles triangles)
• Triangles with all three sides and all three angles equal (similar triangles)

2. Triangle Congruence Theorems: Unit 4 Test Congruent Triangles Answers

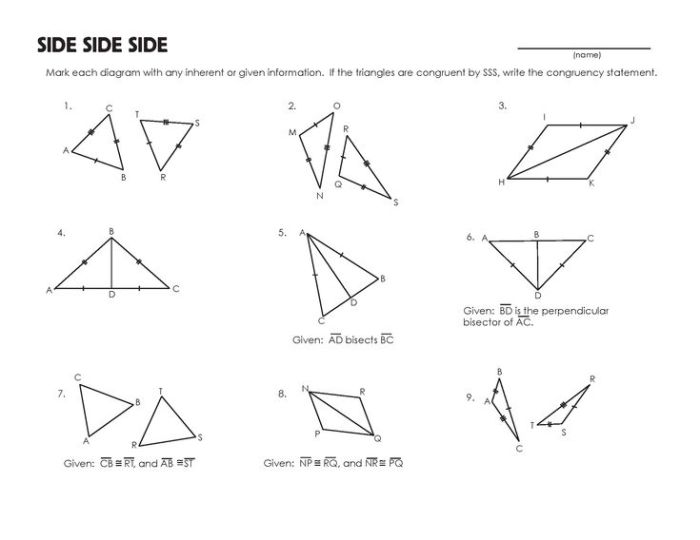
There are three triangle congruence theorems: SSS, SAS, and AAS.

• SSS (Side-Side-Side):If three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent.
• SAS (Side-Angle-Side):If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.
• AAS (Angle-Angle-Side):If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.

3. Methods for Proving Triangle Congruence

There are several methods for proving triangle congruence, including:

• Angle Bisectors:If an angle bisector of a triangle divides the opposite side into two equal segments, then the triangles formed by the angle bisector and the two sides of the triangle are congruent.
• Perpendicular Bisectors:If a perpendicular bisector of a side of a triangle passes through the opposite vertex, then the triangles formed by the perpendicular bisector and the two sides of the triangle are congruent.
• Medians:If a median of a triangle divides the opposite side into two equal segments, then the triangles formed by the median and the two sides of the triangle are congruent.

4. Applications of Triangle Congruence

Triangle congruence has many applications in real-world scenarios, including:

• Construction:Congruent triangles can be used to ensure that buildings and structures are symmetrical and stable.
• Engineering:Congruent triangles can be used to design bridges, airplanes, and other structures that must be able to withstand stress and strain.
• Design:Congruent triangles can be used to create patterns and designs in art, architecture, and fashion.

Key Questions Answered

What is the definition of congruent triangles?

Congruent triangles are two triangles that have the same shape and size, meaning their corresponding sides and angles are equal.

What are the three triangle congruence theorems?

The three triangle congruence theorems are SSS (Side-Side-Side), SAS (Side-Angle-Side), and AAS (Angle-Angle-Side).

How can I use the angle bisector theorem to prove triangles congruent?

If an angle bisector divides two sides of a triangle into proportional segments, then the triangle is congruent to another triangle formed by the angle bisector and the other two sides.