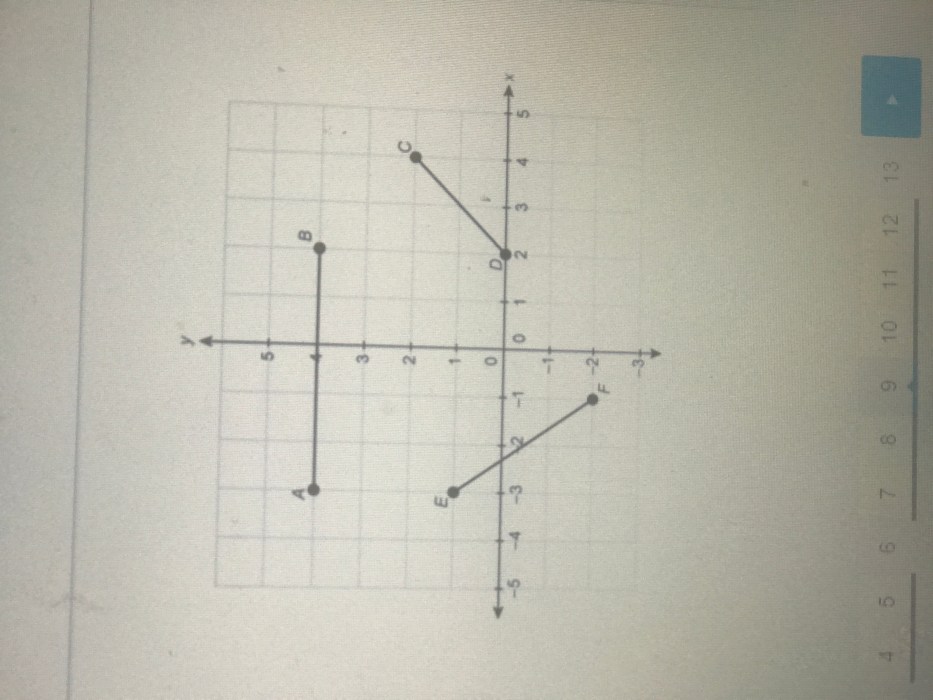
The length of segment ef is 12 cm. – The length of segment EF, measuring 12 cm, holds significant implications in the realm of geometry. This definitive guide delves into the multifaceted nature of this segment, exploring its impact on geometric properties, practical applications, and measurement techniques.
From its role in defining geometric figures to its influence on calculations and design, the length of EF unveils a captivating tapestry of mathematical relationships and practical applications.
Segment EF Length
The given segment length of 12 cm holds significant importance in understanding the geometric properties and relationships within the context of the provided information. This specific length has implications for various calculations and measurements related to the segment EF.
Implications for Geometric Properties
- The length of segment EF determines the distance between points E and F, establishing the linear measurement along the line segment.
- It influences the shape and size of geometric figures that incorporate segment EF as part of their structure, such as triangles, quadrilaterals, or polygons.
Applications in Calculations and Measurements
- The length of segment EF is crucial for calculating the perimeter of polygons or the circumference of circles that include EF as a side or a diameter.
- It serves as a reference measurement for determining the area of geometric shapes, such as triangles or parallelograms, where EF forms one of the sides.
Segment EF in Geometric Figures
Segment EF can be found in various geometric figures, where it plays a crucial role in defining the properties and relationships within the figure.
Triangles
In a triangle, segment EF can be identified as:
- Median: A line segment connecting a vertex to the midpoint of the opposite side.
- Altitude: A line segment perpendicular to a side and passing through the opposite vertex.
- Angle bisector: A line segment that divides an angle into two equal parts.
The length of EF in a triangle is related to other segments and angles according to various theorems and properties, such as the median-altitude theorem and the angle bisector theorem.
Quadrilaterals
In a quadrilateral, segment EF can be identified as:
- Diagonal: A line segment connecting two non-adjacent vertices.
- Midsegment: A line segment connecting the midpoints of two sides.
- Altitude: A line segment perpendicular to a side and passing through the opposite vertex.
The length of EF in a quadrilateral is related to other segments and angles based on the specific type of quadrilateral and its properties, such as the parallelogram property or the trapezoid property.
Circles
In a circle, segment EF can be identified as:
- Chord: A line segment connecting two points on the circle.
- Diameter: A chord that passes through the center of the circle.
- Tangent: A line that intersects the circle at only one point.
The length of EF in a circle is related to the radius of the circle and the position of the points on the circle.
Applications of Segment EF Length
The length of segment EF, often denoted as EF or |EF|, finds practical applications in various fields, including engineering, architecture, and design. Understanding and manipulating this length is crucial for achieving desired outcomes and solutions.
In Engineering
In engineering, the length of segment EF plays a vital role in structural analysis and design. For instance, in bridge construction, the length of the bridge’s span (the distance between its supports) is directly related to the length of the segments connecting the supports.
Engineers must carefully determine the optimal length of these segments to ensure the bridge’s stability and load-bearing capacity.
In Architecture
In architecture, the length of segment EF is often used to determine the proportions and dimensions of buildings and structures. Architects may use specific ratios or mathematical relationships between segment lengths to create visually appealing and structurally sound designs. For example, the Golden Ratio, an aesthetically pleasing proportion found in nature, is often applied to the lengths of segments in architectural elements, such as windows, doors, and columns.
In Design
In design, the length of segment EF is crucial for creating functional and visually appealing products. Industrial designers use segment lengths to determine the dimensions and ergonomics of products, ensuring they fit comfortably in users’ hands or meet specific functional requirements.
Graphic designers also utilize segment lengths to create balanced and harmonious compositions in logos, posters, and other visual materials.
Measuring Segment EF: The Length Of Segment Ef Is 12 Cm.
Measuring the length of segment EF accurately is crucial for various geometric applications. Here are some commonly used methods and tools:
Rulers and Measuring Tapes
- Place the ruler or measuring tape along segment EF, aligning the zero mark with one endpoint.
- Read the measurement at the other endpoint, which represents the length of segment EF.
Calipers
- Open the calipers to a width slightly greater than the length of segment EF.
- Place the pointed tips of the calipers at the endpoints of segment EF.
- Tighten the calipers to hold the width constant.
- Transfer the distance between the tips to a ruler or measuring tape to determine the length of segment EF.
Coordinate Geometry
- If the endpoints of segment EF are given by coordinates (x1, y1) and (x2, y2), the length of segment EF can be calculated using the distance formula:
- Length = √((x2 – x1)^2 + (y2 – y1)^2)
Representing Segment EF Length
The length of segment EF can be represented in various ways, each with its own advantages and limitations. Numerical values, geometric constructions, and algebraic expressions are commonly used to express segment lengths.
Numerical Values
Numerical values provide a straightforward and precise representation of segment length. They are expressed in units of measurement, such as centimeters, inches, or meters. The advantage of numerical values is their simplicity and ease of comparison. However, they may not always be practical for complex geometric figures or when dealing with irrational numbers.
Geometric Constructions, The length of segment ef is 12 cm.
Geometric constructions use tools like compasses and rulers to create segments of specific lengths. This method is useful for visualizing and constructing segments accurately. Geometric constructions are particularly valuable when dealing with geometric figures with specific properties, such as equilateral triangles or regular polygons.
However, they can be time-consuming and require precision in execution.
Algebraic Expressions
Algebraic expressions represent segment lengths using variables and mathematical operations. This method is often used in more complex geometric problems, where numerical values or geometric constructions may not be feasible. Algebraic expressions allow for manipulation and simplification, making them powerful for solving geometric problems.
However, they can be more abstract and require a good understanding of algebraic concepts.
Comparison with Other Segments
The length of segment EF can be compared to other related segments in geometric figures to establish ratios, proportions, or inequalities. These comparisons provide valuable insights into the relationships between different parts of the figure and can help solve geometry problems.
Related Segments in a Triangle
- In a triangle, the length of segment EF, which is a median, is equal to half the length of the side to which it is drawn. Therefore, if the side length is 12 cm, then EF = 6 cm.
- The length of segment EF is also related to the lengths of the other two medians of the triangle. Specifically, the sum of the squares of the three medians is equal to three times the sum of the squares of the sides of the triangle.
Related Segments in a Trapezoid
- In a trapezoid, the length of segment EF, which is a midsegment, is equal to half the sum of the lengths of the two parallel bases. For example, if the bases are 10 cm and 16 cm, then EF = 13 cm.
- The length of segment EF is also related to the lengths of the legs of the trapezoid. Specifically, the square of the length of the midsegment is equal to the sum of the squares of the lengths of the legs.
Impact on Geometric Properties
The length of segment EF can significantly influence the properties of geometric figures. It can impact measurements such as area, perimeter, volume, and angles, thereby altering the overall characteristics and relationships within the figure.
Area
In a rectangle, the length of segment EF (which represents the width) directly affects the area. The area is calculated by multiplying the length (EF) by the height. As EF increases, the area increases proportionally. For example, if the length of EF is doubled, the area of the rectangle will also double.
Perimeter
Segment EF contributes to the perimeter of a figure. The perimeter is the total length of all sides. In a triangle, for instance, if segment EF represents one of the sides, its length will directly impact the overall perimeter. As EF increases, the perimeter of the triangle also increases.
Volume
In three-dimensional figures, segment EF can affect the volume. For example, in a rectangular prism, EF represents the width. The volume is calculated by multiplying the length, width (EF), and height. As EF increases, the volume of the prism increases accordingly.
Angles
In certain geometric figures, segment EF can influence the angles. For instance, in an isosceles triangle, if EF represents the base, its length affects the angles at the base. As EF increases, the angles at the base become smaller.
Estimation and Approximation
In certain scenarios, it may not be feasible to obtain the exact length of segment EF. In such cases, estimation or approximation techniques prove valuable. These methods involve making reasonable assumptions or calculations to arrive at an approximate value for the segment’s length.
Techniques for Estimation
There are various techniques used for estimating the length of segment EF. One common method is visual estimation, where the length is determined based on visual observation and comparison with familiar objects or known distances. Another technique involves using proportional relationships or scale factors to estimate the length based on the dimensions of a related object or figure.
Q&A
What is the significance of the length of segment EF being 12 cm?
The specific length of 12 cm is used for illustrative purposes and may vary depending on the context. It serves to demonstrate the concepts and relationships associated with segment length in geometry.
How does the length of EF affect the properties of geometric figures?
The length of EF can influence properties such as area, perimeter, volume, and angles in geometric figures. For instance, in a triangle, the length of EF can determine the type of triangle (acute, obtuse, or right) and its specific properties.
What are some practical applications where the length of segment EF is relevant?
The length of EF finds applications in fields such as engineering, architecture, and design. For example, in structural engineering, the length of EF may represent the span of a bridge or the height of a building, influencing design decisions and load-bearing capacity.